REGRESI LINEAR

MAKALAH NUMERIK

”REGRESI”

 

DOSEN PENGAMPU:

VELLA ANGGREANA, S.T.,M.T

 

KELOMPOK :

ODY HERLEN JANEWA             213110772

OKTA MASDIYANTI                   213110462

RIZKY ANDREAS H                    213110764

RIZQY HIDAYATULLAH           213110567

ZANWA IFLAMA                         213110267

FAKULTAS TEKNIK

PROGRAM STUDI TEKNIK SIPIL

UNIVERSITAS ISLAM RIAU

PEKANBARU

2023

KATA PENGANTAR

            Puji syukur kami panjatkan kehadirat Allah SWT karena atas rahmat dan karunia-Nya kami dapat menyelesaikan makalah ini dengan semaksimal mungkin dengan judul ”REGRESI”. Sholawat beserta salam semoga tetap tercurah kepada Nabi kita, penutup para Nabi sekaligus satu-satunya Uswatun Hasanah kita sebagai umat muslim, yakni Nabi Muhammad SAW. Tidak lupa pula kami ucapkan terima kasih kepada ibu Vella Anggreana, S.T.,M.T selaku dosen mata kuliah Metode Numerik.

            Dalam penulisan makalah ini, kami menyadari masih banyak terdapat kesalahan serta kekeliruan dalam pembuatan makalah ini, baik itu berkenaan dengan materi pembahasan maupun dengan teknik penulisan. Walaupun demikian, kami sudah berusaha semaksimal mungkin dalam membuat makalah ini. Makalah ini masih sangat jauh dari kata sempurna, karena kesempurnaan hanyalah milik Allah SWT semata. Untuk itu, sangat kami harapkan kritik dan saran bagi kesempurnaan makalah ini. Semoga makalah ini bermanfaat serta dapat menambah wawasan ilmu pengetahuan bagi para pembaca.

 

 

 

Pekanbaru,   Juni  2023

 

DAFTAR ISI 

MAKALAH NUMERIK....................................................................................................... i
KATA PENGANTAR......................................................................................................... ii
DAFTAR ISI................................................................................................................... iii
BAB I PENDAHULUAN
1.1        Latar belakang.................................................................................................... 1
1.2        Rumusan Masalah............................................................................................... 1
1.3        Tujuan............................................................................................................... 1
BAB II PEMBAHASAN
2.1        Regresi Linier..................................................................................................... 2
2.2        Regresi Non Linier............................................................................................... 4
2.3        Regresi Polinomial..............................................................................................  6
BAB III PENUTUP
3.1        Kesimpulan....................................................................................................... 13
3.2        Saran............................................................................................................... 13
DAFTAR PUSTAKA..................................................................................................................... 14

 

 

 

BAB I
PENDAHULUAN

1.1        Latar belakang

Regresi adalah suatu metode analisi yang biasa di gunakan untuk melihat pengaruh antara 2 atau banyak variable. Umumnya, analisi regresi digunakan untuk melakukan prediksi atau ramalan. Sedangkan, hubungan variable tersebut bersifat fungsional yg di wujudkan dalam suatu model matematis. Di dalam artikel ini akan dijelaskan sebuah pendekatan numerik untuk penyelesaian persamaan differensial biasa (PDB) yang di dasarkan pada pendekatan suatu fungsi dan turunannya dengan menggunakan jaringan fungsi radial basis. Solusi dari persamaan tersebut, diperoleh dengan cara mengganti fungsi dan fungsi turunannya dengan sebuah fungsi pendekatan menggunakan jaringan fungsi radial basis (radial basis function). Metode regresi terdiri dari tiga variasi, antara lain linear, linear majemuk, dan nonlinear. Regresi linear sederhana dan linear majemuk sering digunakan. Biasanya, metode non linear berfungsi untuk mengolah kelompok data dengan hubungan antar variabel yang kompleks.

1.2        Rumusan Masalah

Perkiraan hubungan antara waktu pekerjaan dengan luas bangunan yang ingin di bangun.

1.3        Tujuan

Untuk dapat mengetahui waktu perkerjaan dengan luas yang dibangun dengan menggunakan metode regresi, Bentuk-bentuk regresi/curva fitting antara lain:

1)      Regresi Linier

2)      Regresi Non Linier

3)      Regresi Polinomial

BAB II
PEMBAHASAN

Analisis   regresi/curva   fitting   digunakan   untuk   memprediksi/meramalkan suatu permasalahan . Pemakaian analisis regresi tidak terbatas pada ilmu teknik saja, tetapi dapat digunakan pada berbagai bidang ilmu, baik ilmu sosial maupun ilmu ekonomi.

BAB II          

2.1        Regresi Linier

                                                                                       Gambar 2.1

 

Regresi linier

Metode yang digunakan dalam regresi linier adalah Metode Kwadrat Terkecil. Tujuan dari metode ini adalah untuk membuat  kesalahan  yang terjadi sekecil mungkin, seperti terlihat dalam gambar 5.1. Caranya adalah dengan mengkwadratkan kesalahan (D2), dimana;

Dari bentuk regresi:

 Y = a + bx

a dan b harus dibuat sedemikian hingga agar D2 menjadi minimum, sehingga:

Sehingga:

Setelah didapat a dan b, lalu masukkan ke persamaan regresi y = a + bx. Untuk memprediksi apakah garis regresi yang kita buat sudah mempunyai kesalahan yang sekecil mungkin, maka perlu dihitung suatu koefisien yang dinamakan koefisien korelasi (r). Koefisien korelasi mempunyai harga dari 0 – 1. Semakin mendekati nilai 1 maka r nya semakin baik.

Rumus untuk menghitung r adalah:

Dimana:

2.2        Regresi Non Linier

    a)    Fungsi Eksponensial

    Bentuk umum regresi eksponensial: (5.1)

            

    Persamaan (5.1) doubah kedalam bentuk ln: (5.2)

            

    Persamaan (5.2) dapat disederhanakan menjadi:

    P = ln Y    q = x

    A = ln A   B = b

    Sehingga persamaan (5.2) menjadi: (5.3)

    P = A + Bq

    Persamaan (5,3) sudah merupakan bentuk regresi linier. Penyelesaian dapat menggunakan penyelesaian dapat menggunakan  penyelesaian  regresi  linier, sehingga  diperoleh  nilai A dan B.

    Setelah A dan B didapat, maka dilakukan proses inverse sehingga didapatkan nilai a dan b.

            

    Langkah  selanjutnya  adalah  memasukkan  nilai  a dan  b ke persamaan  (5.1), sehingga                diperoleh  y = a e^bx.

    Perhitungan koefisien korelasi r :

            

    b)    Persamaan Berpangkat

    Bentuk umum:

    y = a x b        (5.4)

    Persamaan (5.4) diubah ke dalam bentuk log.

    log y = log a + b log x           (5.5)

    Persamaan (5.5) ditransformasikan menjadi:

    P = log y                  B = b

    A = log a                  q = log x

    Bentuk persamaan yang baru:

    P = A + B q      (5.6)

    Persamaan   (5.6)  sudah  merupakan   bentuk    persamaan       linier,   yang  kalau

    diselesaikan akan diperoleh nilai A dan B.                    

    A dan B selanjutnya diinverse menjadi a dan b:

    A = log a                             a = 10A

    B = b                                   b = B

    Nilai a dan b kemudian dimasukkan ke persamaan (5.4) :

    y = a xb

 

    Menentukan koefisien korelasi: 

                

 

2.3        Regresi Polinomial

           Bentuk umum: (5.7)

            

           Persamaan errornya: (5.8)

            

            

    Nilai x dan y sudah diketahui dari data.Yang perlu dicari adalah nilai a0, a1, a2, …., an,  sedemikian rupa sehingga harga D2 menjadi minimum.

          Bentuk penyelesaian: (5.9)

    Persamaan  (5.9)  merupakan  persamaan  simultan  yang  dapat  diselesaikan dengan Gauss Elimination, Gaus Jordan, Iterasi maupun yang lainnya. Yang didapat dari persamaan (5.9) adalah nilai dari a0, a1, a2, …., an.

Selanjutnya masukkan a0, a1, a2, …., an ke persamaan (5.7).

 

Koefisien korelasi ( r )  dapat dihitung sebagai berikut:

        

    Notasi a0, a1, a2, …., an  menyatakan order polinonial yang akan dihitung.

    Polinomial order 1 menghitung a sampai a1

    Polinomial order 2 menghitung a sampai a2

    Polinomial order 3 menghitung a sampai a3

    Demikian seterusnya.

 

 2.4        Penerapan Regresi Terhadap Terkait Ketekniksipilan

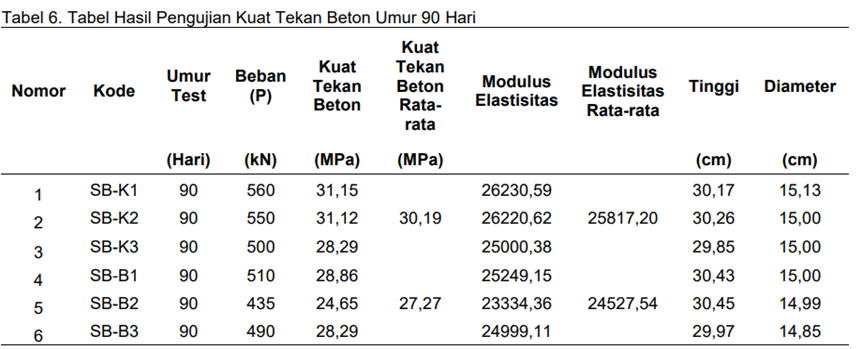
  Dalam Penerapannya kami sebagai penulis, mengkaitkan tentang cara memperkirakan ataupun juga sekaligus mencari hubungan terkait variabel antara Umur Beton dan Kuat Tekan Beton. Sebelum mencari hubungan antara kedua variabel, maka kami sebagai penulis membutuhkan data-data terkait antara kedua variabel tersebut. Dan didapat data antara variabel umur beton dan kuat beton yang dipaparkan di dalam tabel berikut :

            Dari data diatas dapat diketahui bahwa ada tiga jenis beton yang akan kita gunakan untuk mencari hubungan antara variabel umur beton dengan kuat tekan beton. Untuk menentukan variabel yang akan ditentukan, maka kami sebagai penulis hanya memilih salah satu data dari masing-masing tabel kuat tekan beton, yakni 28 hari, 90 hari dan 150 hari. Dan klasifikasi beton yang kami gunakan sebagai variabel adalah jenis beton yang digunakan sebagai pembuatan kolom dengan kode (SB-K). Sebagaimana yang telah dipaparkan pada tabel di bawah ini :

 

Kode	Umur Beton (Hari)	Kuat Tekan Beton
SB-K	28	28.41
SB-K	90	30.19
SB-K	150	31

Setelah data yang didapat dimasukkan ke dalam tabel, maka untuk mencari hubungan terkait dua variabel umur beton dan kuat tekan beton, kita memerlukan variabel-variabel terikat lainnya, yang dipaparkan pada tabel di bawah ini :

Kode	Umur Beton (Hari) (X)	Kuat Tekan Beton (Y)	X.Y	X²	Y²
SB-K	28	28.41	795	784	807.1281
SB-K	90	30.19	2,717	8,100	911.4361
SB-K	150	31	4,650	22,500	961
TOTAL	268	89.6	8,163	31,384	2679.564

Dari data tabel diatas, maka kita dapat mensubtitusikan ke dalam persamaan regresi, yakni persamaan (1) :

Dimana, variabel b dapat kita tentukan dari persamaan (2) :

 dan variabel a juga dapat ditentukan dari persamaan (3) :

Selanjutnya, kita subtitusikan semua data yang sudah didapat di dalam tabel, ke dalam persamaan (2), menjadi

Setelah didapat variabel b, maka lanjutkan untuk mencari variabel a, dengan mensubtitusi nilai b yang sudah didapatkan, menjadi

Setelah didapat nilai dari variabel a dan b, maka didapat lah persamaan regresi, sebagai berikut :

Setelah didapat persamaan regresi, maka kita dapat menentukan hubungan keterkaitan antara variabel umur beton dan kuat tekan beton dengan cara menentukan koefisien korelasi (r), yang didefinisikan dalam persamaan berikut :

Setelah didapat nilai koefisien korelasi (r), maka kita dapat menetukan hubungan antar variabel umur beton dan kuat tekan beton dengan melihat arti nilai koefisien korelasi sebagai berikut :

Dari nilai koefisien korelasi (r) yang didapat, maka dapat ditentukan bahwa hubungan antara variabel Umur Beton dan Kuat Tekan Beton memiliki hubungan yang kuat, yang berarti antara variabel Umur Beton dan Kuat Tekan Beton itu saling memiliki keterkaitan, dimana semakin lama umur suatu beton maka kuat tekannya juga akan semakin besar.

 

 

 

 

 

 

 

 

 

BAB III

PENUTUP

BAB III          

3.1        Kesimpulan

Regresi adalah sebuah metode yang berfungsi untuk memprediksi pengaruh dari dua atau lebih variabel fungsional tertentu. Metode regresi terdiri dari tiga variasi, antara lain linear, linear polinomial, dan nonlinear. Regresi linear sederhana dan linear majemuk sering digunakan. Biasanya, metode non linear berfungsi untuk mengolah kelompok data dengan hubungan antarvariabel yang kompleks. Metode regresi terdiri dari tiga variasi, antara lain linear, linear majemuk, dan nonlinear. Regresi linear sederhana dan linear majemuk sering digunakan. Biasanya, metode non linear berfungsi untuk mengolah kelompok data dengan hubungan antarvariabel yang kompleks.

 

3.2        Saran

Materi regresi merupakan materi analitis yang berkaitan dengan ketelitan analisis dan juga ketepaan terhadap penyajian variabel-variabel yang

 

DAFTAR PUSTAKA

Adhita, Y. (2014, Juni 17). prezi. Retrieved November 5, 2017, from Analisis Regresi Linear Berganda: https://prezi.com/qbhgvujfym_3/analisis-regresilinear-berganda/

Elviana, E., Saputra, A., & Sulistyo, D. (2019). KORELASI KUAT TEKAN TERHADAP KAPASITAS GESER BALOK BETON DENGAN VARIASI PERAWATAN. INERSIA: lnformasi dan Ekspose hasil Riset teknik SIpil dan Arsitektur, 15(2), 10-22.